Indhold
Numerisk partikelspredningsmodel
Teoretisk grundlag
Sammenligning af partikelmodel og analytisk løsning af advektion-dispersionsligningen
Numerisk partikelspredningsmodel
Teoretisk grundlag
Sammenligning af partikelmodel og analytisk løsning af advektion-dispersionsligningen
Numerisk partikelspredningsmodel
Der er opstillet en numerisk partikelspredningsmodel, for at kunne lave en sammenligning af denne og de øvrige stoftransportmodeller, der undersøges i projektet. Figur I.8.1 viser et oversigtsbillede af den vandløbsstrækning som stoftransporten regnes over.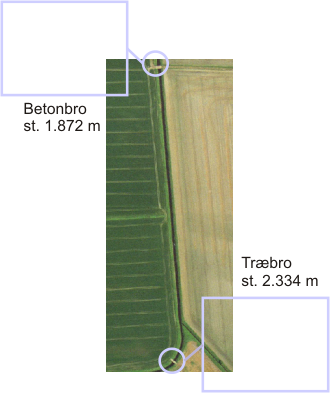


Figur I.8.1: Oversigt over modelområdet med placeringen af henholdsvis betonbroen og træbroen.
Matlab-koden for partikelspredningsmodellen kan hentes her.
Teoretisk grundlag
Der er opstillet en simpel endimensional partikelspredningsmodel for en punktformet udledning i et vandløb. Formålet med modellen er at bestemme diffusionskoefficienten, D, ved brug af målingerne fra rodaminforsøget. Modellen bygger på Ficks 2. lov, ligning I.7.1Skridtlængden for den enkelte partikel beregnes ved ligning I.8.1
Skridtlængde:
(I.8.1)
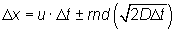
hvor
t er tiden [s]
D er dispersionskoefficienten [m2/s]
u er strømningens middelhastighed [m/s]
±rnd er et tilfældigt genereret tal mellem 0 og 1 [-].
[Larsen]
For at benytte random er det nødvendigt med et par korrektioner, da gennemsnit og varians af en sekvens af random er hhv. 1/2 og 1/12. Derfor benyttes ligning I.8.2 i stedet for ligning I.8.1.
Koncentrationerne udregnes ved at "tælle" antallet af partikler i et givent område. Det ønskes at bestemme koncentrationsforløbet ved betonbroen, x=470 m, og det er valgt at tælle hvor mange partikler, der til hvert tidsskridt befinder sig mellem x=450 m og x=490 m. Det medfører en stedslig udjævning af koncentrationerne at vælge at "tælle" partiklerne indenfor en 40 m lang strækning, men det ville kræve et langt større antal partikler at gøre dette område mindre.
Sammenligning af partikelmodel og numerisk løsning af advektion-dispersions ligningen
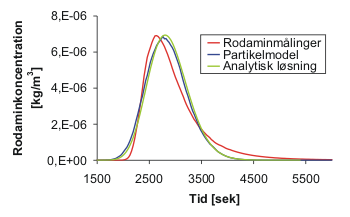 Figur I.8.2: Resultat af beregning med partikelmodel. Figuren viser koncentrationsforløbet
efter 470 m svarende til betonbroens placering.
Stor figur
Figur I.8.2: Resultat af beregning med partikelmodel. Figuren viser koncentrationsforløbet
efter 470 m svarende til betonbroens placering.
Stor figur
-
Tabel I.8.1: Modelinput ved sammenligning af partikelmodel og analytisk løsning af advektion-dispersions ligningen.
- Vandføring [m3/s]Partikelmodellen vurderes at være meget anvendelig til modellering af stoftransporten på delstrækningen i Hasseris Å. Der produceres ingen numeriske fejl og modellen ville let kunne anvendes på ikke stationære beregninger. Til gengæld kræves et stort antal partikler for at udjævne betydningen af de tilfældige tal, men dette betyder samtidig at beregningstiden vil blive stor.
- Tværsnitsareal [m2]
- Dispersionskoefficient [m2/s]
- Transportafstand [m]
- Tilført stofmængde [g]
- Antal partikler
- Tidsskridt [s]
- 0,34
- 2,06
- 0,7
- 470
- 2,253
- 20.000
- 30
[ Til toppen ]
[ Forrige | Næste ] - 0,34
