Indhold
Finitte differens model
Numerisk løsning
- Randbetingelser
- Sammenligning med analytisk løsning
Finitte differens model med magasinering af stof
Resultater
Diskussion
Finitte differens model
Numerisk løsning
- Randbetingelser
- Sammenligning med analytisk løsning
Finitte differens model med magasinering af stof
Resultater
Diskussion
Løsning af advektion-dispersions ligningen med finitte differens metoden
Det er også valgt at lave en numerisk løsning af advektion-dispersions ligningen med finitte differens metoden. Dette gøres med henblik på en sammenligning med de øvrige modeller og for at lave en vurdering af de numeriske fejl, der måtte opstå ved denne løsningsmetode. Det er undersøgt om modellen kan fittes til de målte stofkoncentrationer og hvilke ændringer af modellen, der er nødvendige for at kunne modellere spredning og stoftransport i Hasseris Å.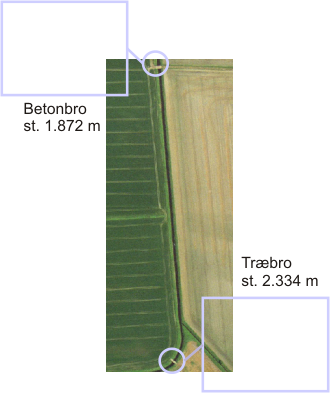


Figur I.9.1: Oversigt over modelområdet med placeringen af henholdsvis betonbroen og træbroen.
Numerisk løsning
Advektion-dispersions ligningen er diskretiseret, så der anvendes fremadrettede differencer i tidsretningen, men centrale differencer i stedsretningen. Dermed kommer advektion- dispersions ligningen til at have følgende form, ligning I.9.1.Advektion-dispersionsligningen på diskret form
(I.9.1)
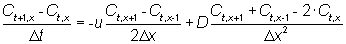
hvor
C er koncentrationen af stof [mg/m3]
t er tiden [s]
x er strømningsretningen i vandløbet
D er dispersionskoefficienten [m2/s]
u er strømningens middelhastighed [m/s].
Randbetingelser
På øvre rand i modellen anvendes ikke centrale differenser, men blot fremadrettede differenser i stedsretningen.
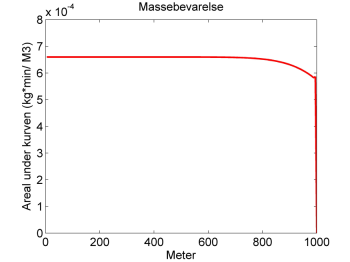
Figur I.9.2: Samlet masse, som passerer et givent punkt i vandløbet. Når der ikke er massebalance i den nederste del af systemet skyldes det at beregningen er stoppet inden alt stoffet har passeret.
Figur I.9.2 viser, at der er massebevarelse i modellen ned til ca. 320 m efter st. 1.872. Når der ikke er massebalance i den sidste del skyldes det, at beregningstiden i dette eksempel var 2 timer og dermed har stoffet ikke nået at passere den nedre del, hvilket også fremgår af ovennævnte videoklip.
Vurdering af numeriske fejl
Først sammenlignes finitte differens modellen og den analytiske løsning af advektion-dispertions ligningen. Hvis de to modeller regner på samme situation må forskellen være et udtryk for de numeriske fejl i finitte differens modellen. I denne sammenligning anvendes følgende input til de to modeller, som vist i tabel I.9.1.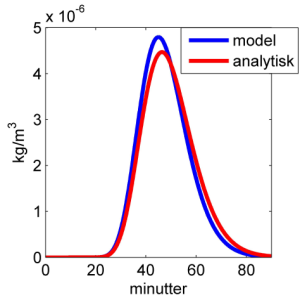
Figur I.9.3: Sammenligning af numerisk og analytisk løsning af advektion-dispersions ligningen.
-
Tabel I.9.1: Modelinput ved sammenligning af analytisk og numerisk løsning
af advektion-dispersions ligningen.
- Vandføring
- Tværsnitsareal
- Dispersionskoefficient
- Transportafstand
- Tilført stofmængde
- Δt
- Δx
- 0,34 m3/s
- 2,06 m2
- 1,7 m2/sek
- 470 m
- 2,253 g
- 10 s.
- 5 m
Den beregnede stofkoncentration efter 470 meters transport ser for de to modeller ud som på figur I.9.3. Det ses umiddelbart, at der er en forskel på de to kurver og at dispersionen er større i den analytiske løsning. Dette skyldes, at FTCS skemaet har en tendes til at "samle" stoffet en smule.
Det er undersøgt, om den samlede stofmængde, der passerer tværsnittet er den samme for de to modeller. Er dette ikke tilfældet er der tale om såkaldte 0. ordens fejl. Det er også undersøgt, om tidsskridtets størrelse har betydning for resultatet. Derfor vises resultater af to kørsler, hvor der er anvendt et tidsskridt på henholdsvis 10 sek og 1 sek.
Det gælder for begge modeller, at den tilførte masse er 2,225 g. Stabilitetskritierierne for finitte differens modellen er i denne sammenligning:
Dermed skulle finitte differens modellen levere stabile resultater. I tabel I.9.2 afvigelsen i den totale stofmængde for de to modeller.
-
Tabel I.9.2: Afvigelsen i den totale stofmængde, der passerer x = 470 m ved den analytiske løsning
og finitte differens modellen.
- dt = 1 sek
- dt = 10 sek
- Analytisk
- 0 kg
- 0 kg
- FD-model
- 3,0 E-08 kg
- 3,2 E-08 kg
Figur I.9.4: Vandplanter langs med bredden af Hasseris Å har væsentlig indflydelse på stoftransporten.
Finitte differens model med magasinering af stof
Det er vist i afsnittet analytisk løsning, at den analytiske løsning ikke helt kunne fittes til de målte stofkoncentrationer, hvilket hænger sammen med den meget forsimplede konceptuelle model. Der er derfor i det efterfølgende lavet en tilføjelse til finitte differens modellen, som tager højde for, at der i kanten af åen er betydeligt lavere hastigheder, end i midterzonen, og at stoffet derfor kan "sætte" sig fast langs bredden.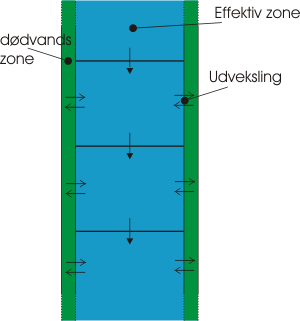
Figur I.9.5: Ny konceptuel model med udveksling mellem "dødvandszone" og den effektive del af vandløbet.
I praksis er dette indført i modellen, ved at tilføje en udveksling af vand mellem en effektiv zone og en "dødvandszone" på hvert steds- og tidsskridt, som illustreret på figur I.9.5 . Efter at den nye koncentration i en boks er udregnet ved advektion-dispersions ligningen udveksles et fast volumen vand (inkl. stof) mellem det strømmende og det stillestående vand. Derved skabes en forsinkelse af en del af stoffet, hvilket øger spredningen/dispersionen.
Resultater
Som det fremgår af figur I.9.6 er det med ovenstående ændring af modellen muligt af fitte modellen til de målte koncentrationer i Hasseris Å. De i tabel I.9.3 opstillede parametre er anvendt og de parametre der fittes på er markeret med fed skrift.
Figur I.9.6: Resultat af stoftransportmodellen inkl. "dødvandszone".
-
Tabel I.9.3: Parametre anvendt ved fit af finitte differens modellen til de målte koncentrationer.
- Vandføring
- Stofmængde
- Dispersionskoefficient, D*
- Δx
- Δt
- Konvektivt couranttal, Ckon
- Diffusivt couranttal, Cdif
- Peclet, Pe
- Areal af effektiv zone
- Areal af dødvandszone
- Udveksling med dødvandszone
- 0,34 m3/s
- 2,25 g
- 0,44 m2/sek
- 5 m
- 10 s.
- 0,36
- 0,18
- 2,0
- 1,87 m2
- 0,29 m2
- 0,045 m3 pr. tids- og stedskridt
* Dispersionskoefficienten giver kun en del af dispersionen. Udvekslingen til dødvandszonen er også en form for dispersion, som ikke er medtaget i D.
Med udvidelsen giver modellen et godt fit til målingerne. Den stejle forkant på grafen sammen med den relativt lange "hale" kan nu begge modelleres med modellen, figur I.9.6.
Diskussion
I første omgang blev der lavet en model, som løste den endimensionale stationære advektion-dispersions ligning numerisk. Det blev konstateret, at resultatet ikke var identisk med den analytiske løsning. Der var ingen afvigelse på stofmængden, men spredningen og skævheden på kurven havde en vis fejl. Disse numeriske fejl er der ikke kompenseret for bevist i den udvidede model. Men ved at tilføje udvekslingen og arealet af dødvandszonen som parametre der kan fittes på, kan modellen tilpasses den målte kurve og de numeriske fejl skjules. Dette ville formentlig blive afsløret, hvis modellen blev valideret mod andre måleresultater på samme vandløbsstrækning. Det havde derfor været ønskeligt at have udført endnu et stoftransportforsøg til validering af modellen.Dispersionskoefficienten, som er bestemt til 0,44 m2/sek, kan imidlertid ikke sammenlignes med den, som er fundet ved de øvrige stoftransportmodeller, fordi en del af spredningen i finitte differens modellen skyldes udvekslingen med dødvandszonen.
[ Til toppen ]
[ Forrige | Næste ]