Teoretisk grundlag
Turbulent strømning
k-Epsilon turbulens model
Smagorinsky turbulens model
Bilag: Turbulensmodeller
Afsnittet bygger på [Brorsen, 2005].Turbulent strømning
Turbulens består af fluktationer i strømningsfeltet i tid og sted opstår når inertikræfterne i væsken bliver vigtige sammenlignet med de viskose kræfter. En turbulent strømning kan beskrives som en tidsligt glattet middelstrømning omgivet af uregelmæssige fluktuationer, som forårsages af hvirvler. Et turbulent hastighedsfelt kan skrives som vist i ligning III.18.1.Hastighedsfeltet i en turbulent strømning:
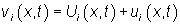
hvor
vi er hastighedsfeltet [m/s]
Ui er middelstrømningen [m/s]
ui er de turbulente fluktuationer [m/s]
Navier-Stokes ligninger gælder for både laminære og turbulente strømninger. Ligningerne kan dog ikke bruges direkte hverken analytisk eller numerisk til at løse en turbulent modellering pga. de mange nødvendige beregningspunkter, som normalt overstiger computernes regnekapacitet. Løsningen er derfor at beskrive middelstrømningen ved Navier-Stokes ligninger, som vist ved ligning III.18.2. Virkningen af de mange hvirvler beskrives på anden vis ved hjælp af turbulens modeller.
Navier-Stokes ligning for turbulent strømning:

hvor
ρ er densitet [kg/m3]
p+ er afvigelsen fra det hydrostatiske tryk [N/m2]
μ er dynamisk viskositet [N*s/m2]
Reynolds-spændingerne:
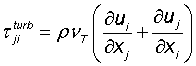
hvor
τjiturb er Reynolds-spændinger [m2/s2]
νT er hvirvelviskositet [N*s/m2]
I det følgende beskrives to forskelige turbulensmodeller som anvendes i delprojektet.
k-Epsilon turbulens model
I k-Epsilon modellen beskrives hvirvelviskositeten som vist i ligning III.18.4.Hvirvelviskositet:
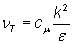
hvor
k er den turbulente kinetiske energi [m2/s2]
ε er den turbulente hvirvelspredning [m2/s3]
Cμ er den turbulente hvirvelspredning på 0,09 [-]
Transportlingninger i k-Epsilon modellen:
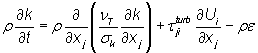
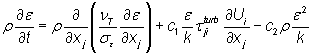
hvor
σk og σε er konstanter, der er indført for at give mulighed for at kompensere for fejl, og er på hhv. 1,0 og 1,3 [-].
C1 og C2 er konstanter på hhv. 1,44 og 1,92 [-]
Smagorinsky turbulens model
Baggrunden for dette teoriafsnit er baseret på manualerne fra henholdsvis MIKE3 og CFX, [MIKE3, 2005], [Ansys CFX, 2005].Andrei Kolmogorov kom i 1941 med en hypotese om, at i en strømmende væske, hvor der opstår store hvirvler vil der efterfølgende generes mindre efterfølgende hvirvler. Det sker ud fra en energibetragtning, hvor store hvirvler får energi fra strømningen. Denne energi anvendes til at skabe selve hvirvlen og den overskydende energi anvendes til at genere mindre og mindre hvirvler osv. indtil energien er opbrugt og forsvinder som varmetab. Dette er forsøgt illustreret på figur III.18.1, hvor energien er optegnet som en funktion af den reciprokke længde af hvirvlerne.
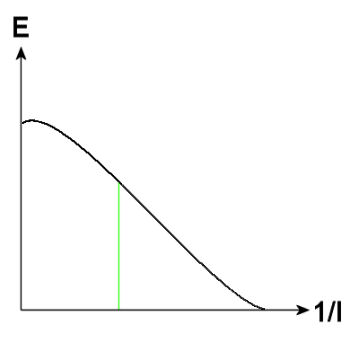
Figur III.18.1: Energien for hvirvler optegnet som en funktion af den reciprokke længde. Den grønne linie symboliserer gridstørrelsen, hvor det der ligger til venstre er store hvirvler.
Til beregningen af turbulente strømninger er der opstillet forskellige modeltyper og beregningsformler og i 1963 kom yderlig en løsning på denne problematik. Det var en meteorologprofessor ved navn Joseph Smagorinsky. Han havde en løsningtil, at medtage de mindre hvirvler, der normalt ville blive forkastet. Smagorinsky modellen er en af de mest anvendte turbulensmodeller når der regnes på turbulente strømninger. Dette skyldes at den er forholdsvis simpel og hovedsageligt kun anvender lokale ændringer til, at beregne forskydningen i væskerne. Dette gøres, når hvirvlerne er mindre end cellestørrelsen, også kaldet en subgrid scale model (SGS). Modellen anvender formlen for Renolds spændinger til beregning af de små hvirvler. Ellers benytter den Navier-Stokes ligningerne. Hvirvelviskositeten beregnes som vist i formel III.18.7:
Ligningen for hvirvelviskositeten i turbulente strømninger, ved hvirvler mindre end gridstørrelsen:
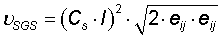
hvor
νSGS er viskositet for subgrid scale [m2/s]
Cs er smagorinsky konstanten [-]
l er hvirvellængden[m]
eij er deformationshastighedstensoren [s-1]
i og j er de respektive retninger
Den generelle formel for deformationshastighedstensoren:
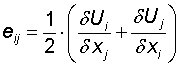
hvor
U er middelhastigheden i det pågældende punkt [m/s]
Beregningen for forskydningsspændingen i Smagorinsky modellen:
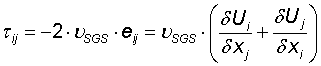
hvor
τ er forskydningsspændingen [m2/s2]
[ Til toppen ]
[ Forrige | Næste ]