Indhold
Validering af strømningsmodel mod GMS
Sammenligning af randbetingelser
Scenarie 1
Scenarie 2
Validering af strømningsmodel mod GMS
Sammenligning af randbetingelser
Scenarie 1
Scenarie 2
Validering af strømningsmodel mod GMS
Det er kontrolleret om strømningsmodellen er opsat korrekt, ved at sammenligne de beregnede trykniveauer med resultatet af en tilsvarende opsætning i GMS. Først undersøges, om definitionen af randbetingelserne er i orden. Dernæst testes 2 scenarier, som ikke har relation til målingerne i laboratoriet, men som blot er opstillet for at teste om modellerne regner ens.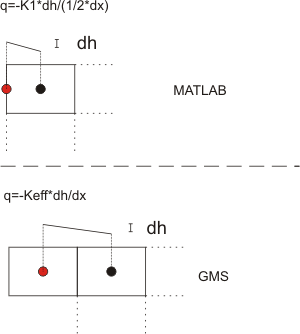
Figur II.10.1: Forskellige måder at definere rande i GMS og egen strømningsmodel (MATLAB).
Sammenligning af randbetingelser
Opsætningen af randene i modellerne er ikke lavet helt på samme måde. I MATLAB er afstanden til de kendte trykniveauer på randene sat til ½ dx, idet trykniveauet er kendt lige op til grænsen af de yderste celler. I GMS er randen derimod defineret i en ekstra søjle celler og dermed bliver afstanden til randen 1 dx. Der kompenseres for denne forskel ved at sætte konduktiviteten i randcellerne i GMS til 1. For at de to måder at definere randene på skal give samme resultat må den effektive konduktivitet, der beregnes i GMS være 2 · K1, hvilket kan udledes af figur II.10.1 og ligning II.10.1
Sammenligning af randbetingelser i MATLAB og GMS.
Hvis vandføringen skal blive ens i de to modeller gælder:
(II.10.1)

Udregning af Keff
(II.10.2)
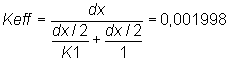
Scenarie 1
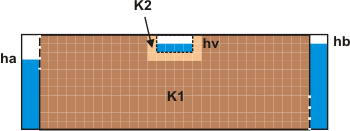 Figur II.10.2: Modelskitse med ha, hb, hv, K1 og K2 markeret.
Figur II.10.2: Modelskitse med ha, hb, hv, K1 og K2 markeret.
-
Tabel II.10.1: Parametre anvendt ved scenarie 1 ved sammenligning af GMS og egen strømningsmodel
- K1
- K2
- ha
- hb
- dx & dy
- 0,001 m2/s
- 0,0001 m2/s
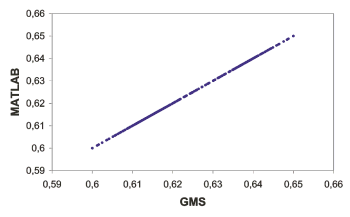 Figur II.10.3: Trykniveauer for scenarie 1 beregnet i henholdsvis
GMS og MATLAB plottet mod hinanden. R-værdien
er 1,00
Figur II.10.3: Trykniveauer for scenarie 1 beregnet i henholdsvis
GMS og MATLAB plottet mod hinanden. R-værdien
er 1,00
- 0,60 m
- 0,65 m
- 0,05 m
Det er også undersøgt, om den beregnede vandføring stemmer overens i de to modeller. Her er en lille, men ubetydelig forskel, som måske kan tilskrives randbetingelserne. Vandføringerne fremgår af tabel II.10.2.
-
Tabel II.10.2: Flow ind og ud af randene i henholdsvis GMS- og MATLAB beregningerne.
- [m3/s]
- Qa
- Qb
- GMS
- -5,2479E-06
- 5,2479E-06
- MATLAB
- -5,2482E-06
- 5,2482E-06
- Forskel
- 3,79E-10
- 3,79E-10
Scenarie 2
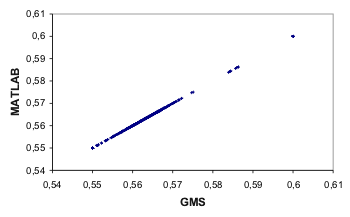 Figur II.10.4: Trykniveauer for scenarie 2 beregnet i henholdsvis
GMS og MATLAB plottet mod hinanden. R-værdien
er 1,00
Figur II.10.4: Trykniveauer for scenarie 2 beregnet i henholdsvis
GMS og MATLAB plottet mod hinanden. R-værdien
er 1,00
-
Tabel II.10.3: Parametre anvendt ved scenarie 2 ved sammenligning af GMS og egen strømningsmodel
- K1
- K2
- ha
- hb
- hv
- dx & dy
- 0,001 m2/s
- 0,0001 m2/s
- 0,55 m
- 0,55 m
- 0,60 m
- 0,05 m
-
Tabel II.10.4: Flow ind og ud af randene i henholdsvis GMS- og MATLAB beregningerne.
- [m3/s]
- Qa
- Qb
- Qv
- GMS
- -4,7753E-06
- -4,7320E-06
- 9,5060E-06
- MATLAB
- -4,7755E-06
- -4,7325E-06
- 9,5080E-06
- Forskel
- 1,45E-10
- 1,44E-10
- -2,89sE-10
Der er naturligvis ingen garanti for, at den konceptuelle model holder og at modellen kan valideres i forhold til de forsøg der er lavet, men selve den nummeriske model beregner samme værdier, som GMS.
[ Til toppen ]
[ Forrige | Næste ]