Bilag: Teoretisk grundlag
Partikelmodellen er opstillet som en numerisk finitte differensmodel, med en fast tidslig og stedlig diskretion svarende til strømningsmodellen. Flytningen af en partikel sker dels ved advektiv transport og ved diffusion/dispersion. Den advektive transport i modellen er beregnet ud fra det todimensionale hastighedsfelt i strømningsmodellen.Advektiv transport
I partikelmodellen beregnes transporten separat for henholdsvis x og y retningen til et givet tidsskridt, ligning II.22.1, figur II.22.1.
Figur II.22.1: x og y retning, som det er anvendt i partikelmodellen.
(II.22.1)
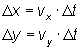
hvor
Δx er ændringen i afstanden i x retningen [m]
Δy er ændringen i afstanden i y retningen [m]
vx er Darcy hastigheden i x retningen [m/s]
vy er Darcy hastigheden i y retningen [m/s]
t er tiden [s].
[Spitz og Moreno, 1996]
Dispersion
Dispersion beregnes som dispersiviteten multipliceret med hastigheden, ligning II.22.2. Det betyder, at dispersionen varierer igennem hele modellen, fordi hastigheden er forskellig fra celle til celle. Det antages at dispersiviteten τD er ens i x og y retningen.(II.22.2)
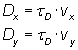
hvor
D er dispersionskoefficienten i henholdsvis x og y retning [cm]
τD er dispersiviteten i henholdsvis x og y retning [cm2/s]
v er hastigheden [cm/s].
[Spitz og Moreno, 1996]
Random Walk metoden
Flytningen af en partikel beregnes ved Random Walk metoden i begge retninger ved ligning II.22.3. Flytningen af en partikel udgøres både af en advektiv transport og en dispersiv transport. På den dispersive transport genereres et tilfældigt uafhængigt tal fra -1 til 1. Darcyhastigheden divideres med effektiv porøsitet for at opnå den reelle hastighed.(II.22.3)
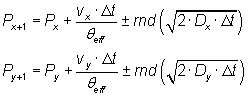
hvor
Px er partiklens placering i x retning [cm]
Py er partiklens placering i y retning [cm]
±rnd er et tilfældigt tal i intervallet 0 til 1 [-]
Θeff er den effektive porøsitet [-].
[Spitz og Moreno, 1996]
[ Til toppen ]
[ Forrige | Næste]