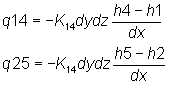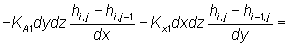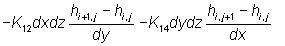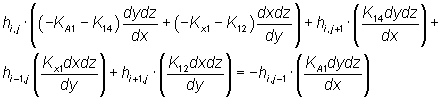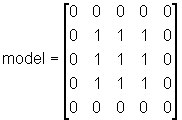Bilag: Teori og opsætning af strømningsmodel
Der er opsat en finitte differens model med det formål at kunne modellere vand-
og stoftransporten i 'sandkassen'. I finitte differens modellen
opdeles 'sandkassen' i mindre celler i et rektangulært grid.
Der opstilles Darcyligninger for vandtransporten mellem cellerne,
og derefter opstilles vandbalancen for hver celle. Det giver ’n’ ligninger
med ’n’ ubekendte, hvor de ukendte størrelser er trykniveauerne i de enkelte celler.
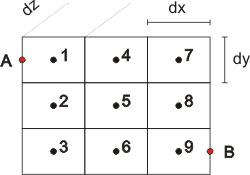
figur II.21.1: Eksempel på simpel grundvandsmodel for 'sandkassen'
med 9 celler og 2 randceller.
I det følgende gennemgås opstillingen af ligningerne for en forsimplet
model med 3 x 3 celler. Det vises ligeledes hvordan opsætningen i praksis
er automatiseret i MATLAB. Selve 'sandkassen' består her af de 3 x 3 celler
med ukendte trykniveauer og derudover er der 2 randbetingelser, hvor trykniveauet
er kendt henholdsvis A og B.
Modellen er opstillet som vist på figur II.21.1.
Darcyligningerne
Vandføringen mellem to celler er proportional med trykgradienten ifølge
Darcy’s lov. Dermed antages det, at sandet indenfor hver celle er
homogent og at strømningen med tilnærmelse kan beskrives ved en
middelhasighed over tværsnitsarealet, ligning (II.21.1) og (II.21.2).
Darcyligninger for lodret vandtransport
(II.21.1)

osv...
Darcyligninger for vandret vandtransport
(II.21.2)
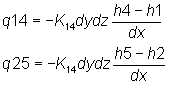
Massebalancer
For hver af de 9 celler med ukendt trykniveau er massebalancen opstillet:
Idet modellen er stationær gælder Q
ind = Q
ud, ligning (II.21.3).
Eks: Massebalance for celle 1, figur II.21.1
(II.21.3)


I massebalancen for celle 1 ses det, at der indgår 3 Darcyligninger.
Da celle 1 ligger i øverste række er der ingen bidrag fra en celle ovenfor.
Det ønskes at lave en metode til at opstille massebalancen for alle celler
på samme måde samtidig med, at der tages højde for særtilfældene ved modellens rand.

Figur II.21.2: Definition af i og j retning.
Denne massebalance for celle 1 omskrives så der anvendes indeks (i, j),
figur II.21.2. Det har vist sig at være hensigtsmæssigt, at lade i være positiv
nedad og j positiv mod højre, idet i, j på denne måde kan henvise til
rækker og søjler i matricen.
Der er herunder, for det generelle tilfældes skyld, tilføjet et flow fra cellen
ovenover (i-1, j), ligning (II.21.4), som dog i dette tilfælde er lig med 0, da vi befinder
os i øverste række.
Massebalance for celle 1, hvor indeks i, j anvendes
(II.21.4)
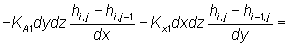
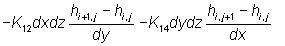
Ovenstående massebalance omstruktureres, så de kendte trykniveauer står på
højre side af lighedstegnet og de ukendte på venstre side. I eksemplet
er h
i, j-1 kendt, idet det er trykniveauet i A, ligning (II.21.5).
Omstrukturering af ovenstående ligning, så kendte trykniveauer er isoleret
på venstre side og ukendte på højre side af lighedstegnet.
(II.21.5)
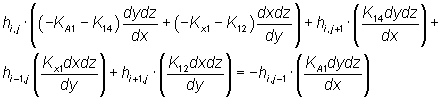
Som det fremgår skal der findes en effektiv konduktivitet på grænsen mellem
alle celler i modellen. Der er i praksis opstillet en matrice, som indeholder
en konduktivitet for hver celle. Dernæst er der lavet 2 nye matricer, hvor
K
eff i henholdsvis x- og y-retningen er beregnet ved et harmonisk gennemsnit.
Matricerne med de effektive konduktiviteter ganges nu på de respektive konstanter, ligning (II.21.6).
Opstilling af koefficienter.
(II.21.6)

Dermed er det nu gjort mere overskueligt, at opstille et ligningssystem
bestående af en koefficientmatrice, A, med n rækker og n søjler,
en h vektor med alle de ukendte trykniveauer og en D vektor, som indeholder
de kendte størrelser (indeholder randbetingelserne).
Koefficientmatricen A:
De røde koefficienter er lig med 0 fordi de pågældende celler
ligger udenfor modelområdet. De blå koefficienter i A matricen er sat til
nul, men medtages i D på højre side af lighedstegnet fordi de henviser
til randceller med kendte trykniveauer.

I cellerne, som grænser op til modellens rand opstår et behov for at
sikre sig, at der ikke kan forekomme et flow ud over randen. Eksempelvis
skal det i matricens første række sikres, at C
i-1, j bliver 0 da der ikke
findes en celle over celle 1. Dette er gjort ved at oprette en matrice
med 3+2 rækker og 3+2 søjler som har 1-taller i de 9 aktive celler og nuller
i de omkringliggende celler. Når koefficienterne udregnes går programmet
først ind på det rigtige sted i model-matricen og kobler cellen til eller
fra ved at gange med 0 eller 1. Bemærk at randcellerne også får værdien 0,
idet disse bidrag i stedet er medtaget i D-vektoren.
Hjælpematrice kaldet "model", hvor
aktive celler har værdien 1
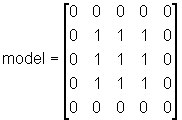
Denne løsning kan dog ikke bruges ved udregning af C
i,j –koefficienterne.
I C
i,j –koefficienterne indgår et bidrag fra hver omkringliggende celle.
Dette bidrag skal indgå i A matricen i de tilfælde, hvor der henvises til en
randcelle. I disse situationer er jo det ukendte trykniveau i celle i, j der
ganges på, hvorfor denne værdi ikke skal stå i D vektoren. Derfor er der
lavet en model(ij) matrice, som sørger for dette. Det skal bemærkes, at
randcellerne her har værdien 2. 2-tallet bliver ganget på K
eff hvorved der
korrigeres for, at afstanden ud til det kendte trykniveau ved randen kun er ½ dx.
Når C
i,j koefficienterne udregnes skal der dermed hentes en værdi fra den
tilhørende celle i model(ij). I den ”ikke forsimplede” udgave af grundvandsmodellen
er vandløbet også defineret som rand ved at indsætte 2-taller i randcellerne.
Hjælpematrice kadet "model(ij)", hvor
aktive celler har værdien 1 og randceller har
værdien 2 (tager højde for ½ dx)

De to model-matricer danner grundlag for oprettelse af K
eff matricerne og sikrer,
at K
eff = 0 når der indgår en celle, der ligger udenfor modelområdet eller medtages i D-vektoren.
Med A-matricen og D-vektoren korrekt opstillet kan de ukendte trykniveauer bestemmes i ligning (II.21.7) ved at invertere A matricen.
Isolering af hvektoren
(II.21.7)

I MATLAB kan samme resultat opnås ved at bruge en indbygget algoritme, som bestemmer
h ved den mest egnede iterationsmetode.
Dette er tidsbesparende i forhold til en traditionel invertering af A-matricen.
Ved at opstille ligningssystemet som beskrevet, kan opsætningen af A, h og D
automatiseres i MATLAB, så det kun er nødvendigt at definere antallet af rækker
og søjler, samt hvilke celler, der er randceller.
For mere detaljeret gennemgang af hvordan programmet er lavet henvises til selve
programkoden, som også indeholder forklarende kommentarer.
Modelkode.
[
Til toppen ]
[
Forrige |
Næste ]

 osv...
osv...