Beskrivelsen af de turbulente strømninger sker gennem turbulensmodeller, hvor hvirvelviskositeten, n_T, er bestemt. Hvirvelviskositeten benyttes efterfølgende til at beregne de turbulente forskydningsspændinger, som beskriver effekten af fluktuationerne, og dermed udvekslingen af bevægelsesmængde på tværs af strømningsretningen, som forårsages af turbulensen. Ved brug af turbulensmodeller, som således beskriver en relation mellem middelstrømning og Reynolds-spændingerne, er det kun nødvendigt at beskrive middelstrømningen for at bestemme hvirvelviskositeten. I turbulensmodellerne bestemmes hvirvelviskositeten på forskellige måder. De opstillede turbulensmodeller bør overholde kravet n_T>0, da tilstedeværelsen af hvirvler altid vil give en opblanding på tværs af strømningsretningen. [Brorsen, 2003]

I nedenstående afsnit er k-modellen, ke-modellen, Smagorinsky-modellen og kombineret 1D ke- og 2D Smagorinsky-modellen beskrevet.

k-modellen
I k-modellen er hvirvelviskositeten bestemt med udgangspunkt i den turbulente kinetiske energi.

hvor	nT ld k	er hvirvelviskositeten [m2/s] er længdeskalaen for de turbulente hvirvler [m] er den tidsligt glattede turbulente kinetiske energi [m2/s2]

For at bestemme hvirvelviskositeten er der i k-modellen opstillet en transportligning for den turbulente kinetiske energi, k, og i MIKE 3, som i dette projekt er benyttet til modellering af turbulens, er denne transportligningen løst som: [DHI, 2003]

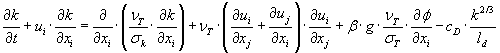hvor	t u x sk sT b g f cD	er tiden [s] er hastigheden [m/s] er stedet [m] er en empirisk konstant [-] er en empirisk konstant [-] er den volumetriske udvidelseskoefficient [-] er tyngdeacclerationen [m/s2] er buoyancy scalar quantity [-] er en empirisk konstant  [-]

Når k er fundet, kan hvirvelviskositeten bestemmes ud fra en kendt længdeskala for de turbulente hvirvler, l_d.

Et problem ved brug af k-modellen er imidlertid, at der i generelle strømningstilfælde kun er ringe kendskab til l_d. Dette bevirker, at k-modellen ofte ikke giver væsentligt bedre resultater end blandingslængde-modellen, som ikke benytter den turbulente hastighedsskala, hvormed modellen kan forudsige hvirvelviskositeter lig med 0, hvilket ikke er muligt ved turbulente strømninger. [Brorsen, 2003]
På grund af dette, er denne model ikke benyttet ved beskrivelsen af strømningsproblemet i dette projekt.
 

ke-modellen
I modsætning til k-modellen, er der i ke-modellen udover en transportligning for den turbulente kinetiske energi, også opsat en transportligning, så længdeskalaen for de turbulente hvirvler, l_d, kan bestemmes. Denne transportligning er opskrevet for dissipationen, e, hvorudfra længdeskalaen for de turbulente hvirvler kan findes, når den turbulente kinetiske energi er bestemt [Brorsen, 2003]:

hvor	e A	er dissipationen [m2/s3] er en konstant lig med 0,09 [-]

I MIKE 3 er transportligningen for den turbulente kinetiske energi opstillet som: [DHI, 2003]

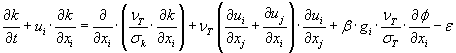Og transportligningen for dissipation er opstillet som: [DHI, 2003]

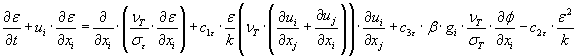hvor	t se c1e c2e c3e	er tiden [s] er en empirisk konstant [-] er en empirisk konstant [-] er en empirisk konstant [-] er en empirisk konstant [-]

Når disse to transportligninger er løst, kan hvirvelviskositeten, n_T, bestemmes:

hvor	cm	er en empirisk konstant [-]

Denne model er benyttet ved modelleringen af de turbulente strømninger i strømrenden. Det ses dog, at modellen indeholder en række empiriske konstanter, hvis størrelse bygger på en lang række forsøg. Dette vanskeliggør en egentlig kalibrering af modellen, hvorfor resultaterne, der fremkommer med en standardopsætning, som udgangspunkt, må accepteres.   

Smagorinsky-modellen
Smagorinsky-modellen er den mest anvendte turbulensmodel. I denne model er hvirvelviskositeten, n_T, beregnet af ændringer i hastighedsfeltet. Hvirvelviskositeten beregnes som:

hvor	nT Cs D Sij	er hvirvelviskositeten [m2/s] er Smagorinsky's konstant [-] er boksstørrelsen [m] er deformationshastighedstensoren [s-1]

Deformationshastighedstensoren beskriver ændringerne i hastighedsfeltet og er bestemt af:

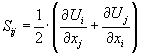hvor	U x	er hastighedskomposanten [m/s] er retningen

I Smagorinsky-modellen er der i beregningen af hvirvelviskositeten også taget hensyn til, hvilke hvirvelstørrelser der medtages i beregning af Reynoldsspændingerne. Dette er gjort ved at inkludere boksstørrelsen, D, i formlen for hvirvelviskositeten, hvormed små hvirvler mindre end boksstørrelsen beregnes som Reynoldsspændinger, mens større hvirvler indgår i Navier-Stokes ligning som en del af middelstrømningen.

Smagorinsky-modellen  er benyttet ved modelleringen af de turbulente strømninger i strømrenden. Her er det muligt at kalibrere modellen ved justering af Smagorinsky konstanten C_s.

Kombineret 1D ke og 2D Smagorinsky modellen
I den kombinerede 1D ke- og 2D Smagorinsky model, beregnes hvirvelviskositeten i den horisontale udstrækning vha. Smagorinsky-modellen, og i den vertikale udstrækning ved ke-modellen.

Kombineret 1D ke- og 2D Smagorinsky modellen er specielt anvendelig når den horisontale gridudbredelse er meget større end den vertikale gridudbredelse. Dette gør modellen velegnet ved modellering af eksempelvis fjorde og større havområder, da der her netop er en meget stor horisontal udbredelse i forhold til den vertikale udbredelse.

I MIKE 3 er der benyttet en transportmodel for k som vist nedenfor: [DHI, 2003]

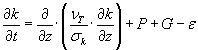hvor	P G	er bidrag fra hastighedsforskydning [m/s] er bidrag fra opdrift [-]

P og G er beregnet som:

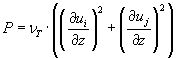hvor	u	er hastigheden i den horisontale retning [m/s]

hvor	g r sT	er tyngdeaccelerationen [m/s2] er densiteten [g/m2] er Prandtl's tal [-]

 
Og transportmodellen for e er:

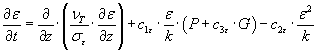I strømrenden er den horisontale gridudbredelse ikke meget større end den vertikale gridudbredelse, hvorfor den kombinerede 1D ke- og 2D Smagorinsky model ikke er anvendt til løsning af strømningsproblemet i dette projekt.

Med udgangspunkt i ovenstående er det valgt at benytte ke-modellen og Smagorinsky-modellen til beskrivelsen af de turbulente strømninger i strømrenden, da disse passer bedst med dette strømningsproblem.