hvor
t0
r
g
R
I
er bundforskydningsspændingen [N/m2]
er densiteten [kg/m3]
er tyngdeaccelerationen [m/s2]
er hydraulisk radius [m]
er energiliniegradienten [m/m]
Til bestemmelse af bundforskydningsspændingen ved brug af energiliniegradienten er der med udgangspunkt i en kraftligevægt for et væskelegeme benyttet at: [Brorsen og Larsen, 2001]
|
|
||
|
hvor |
t0 r g R I |
er bundforskydningsspændingen [N/m2] er densiteten [kg/m3] er tyngdeaccelerationen [m/s2] er hydraulisk radius [m] er energiliniegradienten [m/m] |
Det er her antaget, at vandspejlet er sammenfaldende med energilinien, hvorfor en
måling af faldet på vandspejlet hen over de ilagte skærver giver
energiliniegradienten. Det har i den forbindelse vist sig, at der er en stigning
på vandspejlet hen over skærvebunden. Benyttes antagelsen om, at energilinien er
sammenfaldende med vandspejlet, vil energilinien også stige hen over
skærvebunden i strømningens retning, hvilket ikke er korrekt, da energilinien
vil falde i strømningens retning.
Forklaringen på det observerede må være, at der er en større hastighedshøjde i starten af skærvebunden end ved slutningen. Den reducerede hastighedshøjde hen over skærverne er omsat til en stigning i trykhøjden, dvs. en stigning i vandspejlet. Nedenstående principskitse viser situationen.
|
|
| Figur 13 Principskitse af stigende vandspejl og faldende energiliniegradienten. |
På trods af den forøgede trykhøjde, vil energilinien på grund af faldet i
hastighedshøjden falde. For at finde gradienten på energilinien, benyttes, frem
for vandspejlshældningen, energiligningen.
[Brorsen og
Larsen, 2001]
|
|
||
|
hvor |
z p g a V DH |
er referenceniveau [m] er er trykket [m] er specifik tyngde [N/m3] er hastighedsfordelingskoefficienten [-] er middelhastigheden [m/s] er tryktabet [m] |
Da renden er sat med vandret bund sættes z lig nul, og ligningen udtrykker nu,
at trykniveauet plus hastighedshøjden i snit A er lig trykniveau plus
hastighedshøjde i snit B plus det tryktab, der er sket undervejs mellem de to
snit. Isoleres tryktabet mellem to snit, og divideres denne med længden mellem
de to snit, findes energiliniegradienten.
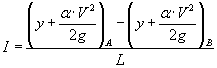 |
||
|
hvor |
y |
er vanddybden i de to snit [m] |
Her beregnes hastighedsfordelingskoefficienten på baggrund af:
|
|
||
|
hvor |
v a A |
er hastigheden i de enkelte punkter [m/s] er arealet tilknyttet de enkelte hastigheder [m2] er tværsnitsarealet af renden [m2] |
Hastighederne i renden er målt i seks punkter i de to tværsnit vha. propel.
Nedenstående figur viser tværsnit A, som blev målt 1,5 m inde i renden, hvilket
svarer til 0,5 m efter skærvebundens start. Vanddybden i tværsnit A er 24,8 cm.
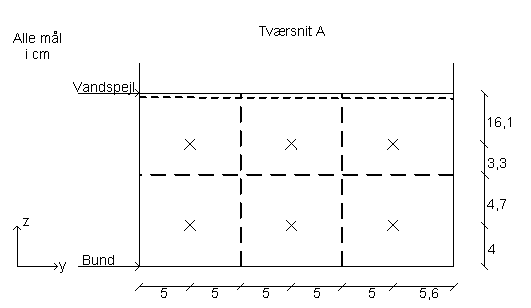 |
| Figur 14 Tværsnit af strømrenden. Krydserne viser hvor propelmålingerne er foretaget, og de stiplede linier afgrænser det areal, som hører til hastighederne målt med propellen. Vanddybden i tværsnit A er 24.8 cm. |
Det andet tværsnit er målt 5 m inde i renden, hvilket svarer til 3,5 m efter skærvebundens start. Vanddybden i tværsnit B er 25,01 cm.
Hastighederne i de to tværsnit er vist i nedenstående tabel:
| Tabel 1 Målte hastigheder i tværsnit A og B. | |||
| Afstand fra kant | Højde over bunden | Hastighed tværsnit A | Hastighed tværsnit B |
| [cm] | [cm] | [m/s] | [m/s] |
| 5 | 4 | 0.259 | 0.233 |
| 5 | 12 | 0.312 | 0.319 |
| 15 | 4 | 0.285 | 0.218 |
| 15 | 12 | 0.314 | 0.341 |
| 25 | 4 | 0.307 | 0.236 |
| 25 | 12 | 0.310 | 0.319 |
Hermed er hastighedsfordelingskoefficienten og dermed hastighedshøjden beregnet
for tværsnit A og B. Resultatet ses i nedenstående tabel.
| Tabel 2 Beregnet hast. fordelingskoefficient og hastighedshøjde for tværsnit A og B. | ||||
| Enhed | Tværsnit A | Tværsnit B | ||
| Vanddybde | y | cm | 24,80 | 25,01 |
| Hast. fordelingskoefficient | a | - | 1,01 | 1,08 |
| Hastighedshøjde | aV2/2g | cm | 0,470 | 0,468 |
Ud fra ovenstående er energiliniegradienten beregnet til -0,7 ‰, hvilket svarer
til, at energilinien stiger
(excelberegning). Dette er ikke korrekt, da energilinien hen over
stykket med skærvebund vil falde pga. den øgede modstand fra skærverne på
bunden. Det negative fald på energilinien kan skyldes, at hastighedshøjderne er
så små, at usikkerhederne ved
måling af højden af vandspejlet overskygger hastighedshøjdens effekt på
energiliniens fald. Dvs. at hastighedshøjderne er så små, at deres betydning
forsvinder i de øvrige usikkerheder, der bl.a. er på måling af vanddybden.
Det er på baggrund af ovenstående valgt ikke at benytte den her beskrevne metode til bestemmelse af bundforskydningsspændingen.