IterationsmetodeVed Gauss-Seidel, som er den mest benyttet iterationsmetoden til modellering af grundvandsstrømningsproblemer, foregår beregningen af trykniveauet systematisk gennem beregningsnettet, hvor beregningen "sweeper" fra venstre mod højre og op. Gauss-Seidel metoden kan udtrykkes som:
På denne måde kan der bruges resultater fra det aktuelle beregningstrin i den aktuelle beregning. Dette gør Gauss-Seidel metoden til en mere effektiv iterationsmetode end f.eks. Jacobi iterationsmetoden, der kun benytter resultater fra det foregående beregningstrin. Metoden kan dog være langsom til at konvergere, hvorfor der indføres en relaxationsfaktor. RelaxationsfaktorForskellen mellem to beregningstrin benævnes residual, som er defineret som:
|
|
|
|
|
Figur 5 Gauss-Seidel iterationsmetoden "sweeper" gennem beregningsnettet fra venstre mod højre linie for linie. |
|
|
Ved at erstatte hi,jm med hi,jm+1 efter hvert beregningstrin stabiliseres residualet ved hver beregningscelle. Ved indførelse af en relaxationsfaktor multipliceres residualet med en relaxationsfaktor, w, hvor w ³ 1.
Indsættes (1.3) i (1.1) fås
Hvis residualet w > 1 , siges det beregnede trykniveau at være over relaxed. Hvis 0 < w < 1 siges det beregnede trykniveau at være under relaxed og hvis w =1 reduceres (1.4) til (1.1). Den bedste metode til fastsættelse af relaxationsfaktoren er manuelt ved "trial and error" metoden, og generelt ligger den mellem 1 og 2. [Wang og Anderson, 1982]
|
||
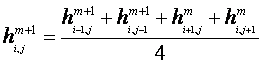 (1.1)
(1.1)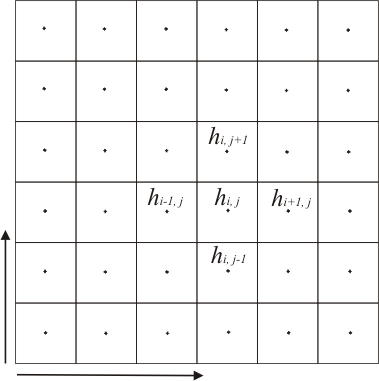
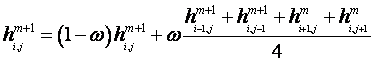 (1.4)
(1.4)